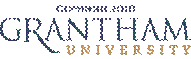Instrumentation and Measurement & Lab – Week #1 Lecture 1

Overview

1.1 Introduction

The technology of controlling a series of events to transform a material into a desired end product is called process control. For instance, the making of fire could be considered a primitive form of process control. Industrial process control was originally performed manually by operators. Their sensors were their sense of sight, feel, and sound, making the process totally operator-dependent. To maintain a process within broadly set limits, the operator would adjust a simple control device. Instrumentation and control slowly evolved over the years, as industry found a need for better, more accurate, and more consistent measurements for tighter process control. The first real push to develop new instruments and control systems came with the Industrial Revolution, and World Wars I and II added further to the impetus of process control. Feedback control first appeared in 1774 with the development of the fly-ball governor for steam engine control, and the concept of proportional, derivative, and integral control during World War I. World War II saw the start of the revolution in the electronics industry, which has just about revolutionized everything else. Industrial process control is now highly refined with computerized controls, automation, and accurate semiconductor sensors.

1.2 Control Systems

Let’s start by discussing an example of a control system that is encountered in everyday life. Consider a simple heating system shown in Figure 1. The house, in a cold climate, can be maintained near a desired temperature by circulating hot water through a heat exchanger. The temperature in the room is determined by a thermostat, which compares the measured value of the room temperature to a desired range, say 64-72 oF. If the temperature below 64, the furnace and pump are turned on, and if the temperature is above 72, the furnace and pump are turned off. If the temperature is between 64-72 oF, the furnace and pump status remains unchanged. This approach is termed “ON/OFF” control and can be used when precise control at the desired value is not required. Based on this example we identify the following common control features:

1. Control system uses a specific value or range as the desired value for the controlled variable. The term set point is usually used for the desired value.
2. The conditions of the system are measured; that’s all control systems use sensors to measure the physical variables that are to be maintained near their desired values.
3. Each control system has a control calculation “algorithm”, which uses the measured and desired values to determine a correction to the process operations. The control calculation for the room heater is very simple (on/off) where the calculations used in other systems may be very complex.
4. The results of the control calculation are implemented by adjusting some item of equipment in the system, which is termed the final control element such as the furnace and pump switches.

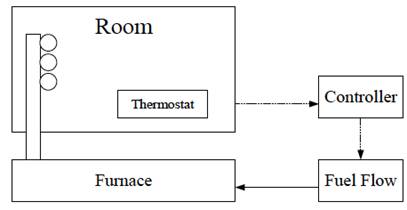
Figure 1: Feedback control for room temperature

These major components are shown schematically in Figure (2), which can be used to represent many control systems.

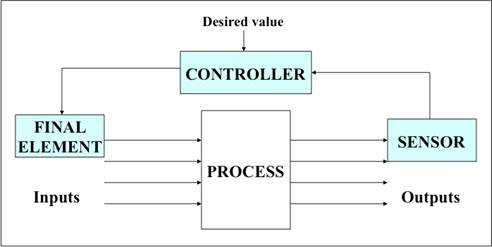
Figure 2: Schematic diagram of general feedback control system

The given control example have an additional feature that is extremely important. This is feedback, which is defined as follows: feedback control makes use of an output of a system to influence an input to the same system. In our example, the temperature of the room is used, through the thermostat on/off decision to influence the hot water flow to the exchanger. The importance of feedback can be seen by considering the alternative without feedback. For example, an alternative approach for achieving the desired room temperature would set the hot water flow based on the measured outside temperature and a model for heat loss of the house. This type of predictive approach is termed feed-forward control. The strategy without feedback would not maintain the room near the desired value if the model had errors-as it always would. Some causes of model error might be changes in external wind velocity and direction or inflows of air through open windows. On the other hand feedback control can continually manipulate the final control element to achieve the desired value. Thus, feedback provides powerful feature of enabling a control system to maintain its desired value without requiring an exact plant model.

When used in discussing control systems the terms input and output do not necessarily refer to material moving into and out of the system. Here, the term input refers to a variable that causes an output. In the room heating example, the input is the fuel to the furnace, and the output is the room temperature. The casual relationship inherent in the physical process forces us to select the input as the manipulated variable and the output as the measured variable.

1.2.1. Process – Control Principles

A key factor in engineering is the design of the process so that it can be controlled well. A more responsive plant would be easier to control. By responsive we mean that the controlled variable responds quickly to adjustments in the manipulated variable. Also, a plant that is susceptible to few disturbances would be easier to control. Reducing the frequency and magnitude of disturbances could be achieved by many means; a simple example is placing a large mixing tank before a unit so that feed composition upsets are attenuated by the averaging effects of the tank.

1.2.2 Servomechanisms

Another commonly used type of control system, which has a slightly different objective from process control, is called a servomechanism. A servomechanism, sometimes shortened to servo, is an automatic device that uses error-sensing negative feedback to correct the performance of a mechanism.
The term correctly applies only to systems where the feedback or error-correction signals help control mechanical position, speed or other parameters. For example, an automotive power window control is not a servomechanism, as there is no automatic feedback that controls position—the operator does this by observation. By contrast a car's cruise control uses closed loop feedback, which classifies it as a servomechanism.

Figure 3: Servomotor

1.2.3 Discrete-State Control Systems

Discrete-state control systems control a sequence of events, rather than regulation or variation of individual variables. The starting and stopping of events is a discrete-based system. The event is either true of false. This type of control system can also be made automatic and is perfectly suited for computer-based controllers.

1.3 Process-Control Block Diagram

As in other systems, a block diagram may be used to model the process control system.

1.3.1 Identification of Elements

Process - The system which is controlled is called the process, or sometimes the plant. The output of the process is the variable or variables, such as the temperature, level, flow, pH or pressure, which are desired to be controlled or regulated. For example, to control temperature, heat must be added or removed from a volume of chemical. The process may consist of the flow of steam or the flow of cooling liquid or both. How the chemical responds to more steam flow or more cooling liquid is the process.

Measurement - The conversion of the variable into some corresponding analog or digitally encoded signal is a measurement. A sensor or transducer is a device that performs this task. Further transformation may be required or signal conditioning may be needed.

Error Detector - An error detector is required to determine if the measurement from the sensor is above or below the desired setpoint, or if there is no error. In either case the error is the signal that indicates that control action is required.

Controller - The controller examines the input from the error detector and determines what action to take. The controller requires an input of both the measured indication of the controlled variable and a representation of the setpoint.

Control Element - The final element in the process-control operation is the device that exerts a direct influence on the process. The control element may also be referred to as the final control element. Sometimes a device like a motor may be required to control the speed of a conveyor or the position of a valve. This device is referred to as an actuator.

1.3.2 Block Diagram

The block diagram provides a simpler overview of the system to be analyzed.

Figure 5: A practical system

The Loop - The process control block diagram describes the flow of signals from the measured variable to the error detector, the controller and to the final control element. In general, this configuration is referred to as a control loop or feedback loop because we determine an error and feed back a correction to the process.

1.4 Control System Evaluation

The variable used to measure the performance of the control system is the error e(t), which is the difference between the constant set point, or reference value, r, and the controlled variable, c(t).

e(t) = r-c(t).

Since the value of the controlled variable may vary with time, so may be error.

Control System Objective - The objective of a control system is best represented by three requirements:

1. The system should be stable.
2. The system should provide the best possible steady state regulation.
3. The system should provide the best possible transient regulation.

1.4.1 Stability

The purpose of the control system is to regulate the value of some variable. This requires that action be taken on the process itself, in response to a measurement of the variable. If this is done correctly, the control system can cause the process to become unstable. The tighter we try to control the variable, the greater the possibility of system instability. Typically, as the control system is adjusted to give better control, the likelihood of instability also increases.

1.4.2 Steady State Regulation

The steady state error is the error after the transient response has decayed, leaving only the continuous response. In other words, it is the error after everything has settled out. For instance, it might be the error remaining after oscillations in the response have ceased. The objective of the best possible steady state regulation simply means that the steady state error should be a minimum. When a control system is specified, there will be some allowable deviation about the set point. This means that variations of the variable within this band are expected and acceptable.

1.4.3 Transient Regulation

Transient regulation specifies how the control system reacts to bring the controlled variable to the new set point. Another type of transient influence is a sudden change of some other process variable. The controlled variable depends on other process variables. If one of them suddenly changes value, the controlled variable may be driven to change also, so the control system acts to minimize the effect. This is called transient response.

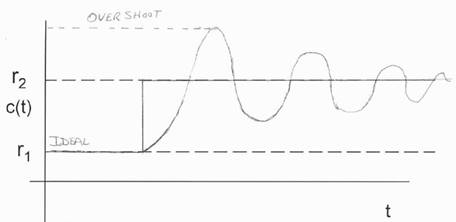
1.4.4 Evaluation Criteria

The question of how well the control system is working is thus by (1) ensuring stability, (2) evaluating steady state response, and (3) evaluating the response to set point changes and transient effects. The term tuning is used to indicate how a process control loop is adjusted to provide the best control.

Damped Response - If a system responds to a set point change or a transient disturbance with an error of only one polarity (no oscillations), the system displays a damped response. Different tuning will provide different values of maximum error.

Cyclic Response - If a system responds to either a set point change or a transient disturbance with an oscillation of the error about the set point, the system displays a cyclic response. Parameters of interest are the maximum error and the duration of the oscillations, also called the settling time. The duration is measured from the time when the allowable error is first exceeded, to the time when it falls within the allowable error and stays. This response is modified by adjusting the control loop parameters, which is called tuning. A number of standard cyclic tuning criteria are used. Two common types are minimum area and quarter amplitude. In minimum area, the tuning is adjusted until the net area under the error time curve is minimum. The quarter amplitude criterion specifies that each peak of the cyclic response shall be a quarter of the amplitude of the preceding peak.

1.5 Analog and Digital Processing

Variables are analog in nature, and before digital processing evolved, sensor signals were processed using analog circuits and techniques, which still exist in many processing facilities. Most modern systems now use digital techniques for signal processing.

1.5.1 Data Representation

Analog Data: Signal amplitudes are represented by voltage or current amplitudes in analog systems. Analog processing means that the data, such as signal linearization, from the sensor is conditioned, and corrections that are made for temperature variations are all performed using analog circuits. Analog processing also controls the actuators and feedback loops. The most common current transmission range is 4 to 20 mA, where 0 mA is a fault indication.

Digital Data: Signal amplitudes are represented by binary numbers in digital systems. Since variables are analog in nature, and the output from the sensor needs to be in a digital format, an analog to digital converter (ADC) must be used, or the sensor’s output must be directly converted into a digital signal using switching techniques. Once digitized, the signal will be processed using digital techniques, which have many advantages over analog techniques, and few, if any, disadvantages. Some of the advantages of digital signals are: data storage, transmission of signals without loss of integrity, reduced power requirements, storage of set points, control of multiple variables, and the flexibility and ease of program changes. The output of a digital system may have to be converted back into an analog format for actuator control, using either a digital to analog converter (DAC) or width modulation techniques.

1.5.2 On/off Control

Room temperature control utilizing a thermostat is an example of on/off control. When the temperature drops below the set point, the thermostat turns the heater on. When the temperature reaches the set point, the thermostat turns the heater off. A dead band could be utilized in the thermostat to establish a temperature range where no action will occur. Hysteresis means that the behavior of the system is different at the same value of temperature, depending on whether the temperature is increasing or decreasing.

1.5.3 Analog Control

True analog control exists when all variables in the system are analog representations of another variable.

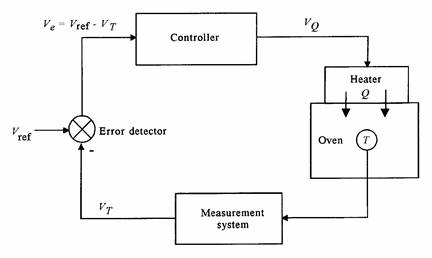
Figure 7: Analog control system such as this allows continuous variation of some parameter, such as heat input, as a function of error.

1.5.4 Digital Control

Digital control involves the use of a computer in modern applications; although in the past, digital logic circuits were also used.

Supervisory Control - Supervisory control means a remotely mounted controller could be monitored from a central location, such as a control room. However, control still is executed at the controller.

Direct Digital Control - As computers have become more reliable and miniaturized, they have taken over the controller function.

Smart Sensor - With microprocessor large-scale integration, the controller can be embedded in the sensor itself. The most current technology today is to interface smart sensors in a local area network or field bus.

Networked Control Systems - In order to have coordinated control throughout a large plant site, digital control units may be placed on a local-area network utilizing a variety of carriers such as fiber optic cables, as well as metallic conductors. The most commonly implemented standards are the Foundation Fieldbus and the Profibus.

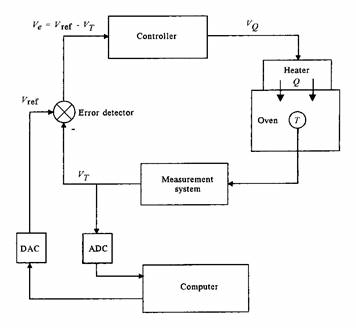
Figure 8: In Supervisory control, the computer monitors measurements and updates setpoints, but loops are still analog in nature.

1.5.5 Programmable Logic Controllers

Manufacturing operations may be on/off in nature. In the past, much of this control utilized relays. Computers have also taken over the operation of such relay logic controllers. Special microprocessor based computers designed for discrete control are called programmable logic controllers or PLC’s.

Figure 9: A Programmable Logic Controller

1.6 Units, Standards, and Definitions

Common units, standards and definitions are utilized in process control.

1.6.1 Units

A particular set of metric units is used, called the international system or SI. It is also important for the process control specialist to know English units and be able to perform conversions between the SI system.

International System of Units - The international system is based on seven well-defined base units in two supplementary, dimensionless units. Please refer to the table on page 22 in the text.

Standard metric prefixes are also applied to the standard units – refer to appendix 1.

1.6.2 Analog Data Representation

For measurement systems or control systems, part of the specification is the range of the variables involved. Two analog standards are in common use as a means of representing the range of variables in control systems. For electrical systems, we use a range of electric current carried in wires; and for pneumatic systems (systems where air pressure and flow are used to measure, control and interact with the process), we use a range of gas pressure carried in pipes.

Current Signal - The most common current transmission signal is 4 to 20ma.

Pneumatic Signals - In the United States, the most common standard for pneumatic signal transmission is 3 to 15 psi.

1.6.3 Definitions

Following are some common terms and expressions used to describe process control elements.

Error - When used for a controlled variable and a control system, error is the difference between the measured value of the variable and the desired value: that is, the reference or set point value.

Block Definitions - Control systems are often described in terms of blocks. One block represents the measurement, one the controller, and so on.

Transfer Function - The transfer function describes the relationship between the input and output for the block. It is usually a mathematical expression that describes the relationship.

Accuracy - Accuracy is used to specify the maximum overall error to be expected from a device. Accuracy is usually expressed as the inaccuracy and can appear in several forms.

1. Measured variable
2. Percentage of the instrument full-scale reading
3. Percentage of instrument span
4. Percentage of the actual reading

System Accuracy - Often, one must consider the overall accuracy of many elements in a process control loop to represent a process variable. The best way to do this is to express the accuracy of each element in terms of the transfer functions.

Sensitivity - Sensitivity is a measure of the change in output of an instrument for a change in input.

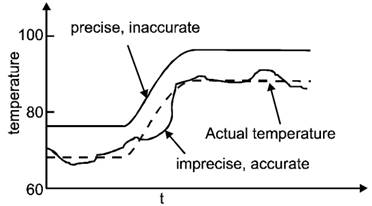
Hysteresis and Reproducibility - An instrument may not have the same output value for a given input in repeated trials. Such variation can be due to inherent uncertainties that imply a limit on the reproducibility of the device. Hysteresis is when a different reading results depending on whether the input value is approached from higher or lower values.

Resolution - Measurement devices have a minimum measurable value of their input variable, which is called the resolution.

Linearity - A linear relationship between two variables results in a straight-line. A linear relationship between input and output is highly desirable.

1.6.4 Process Control Drawings

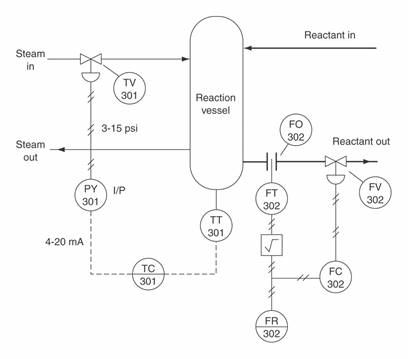
Process control drawings employ a standard set of symbols and definitions to represent a plant and its associated control systems. This standard was developed by the American National Standards Institute and the Instrumentation Systems and Automation Society (ISA). Detailed process control diagrams are shown on what are called piping and instrumentation diagrams or P&ID drawings.

Essential Elements - The P&ID depicts the entire plant and associated control systems. This includes plant operating units, product flow lines, measurement and control signal lines, sensors, controllers, final control elements, computers and programmable logic controllers.

Instrument Lines Symbols - The standard current signal is represented as a dashed line. A pneumatic signal is represented as a line with crosshatches. A digital data line to or from a computer is represented as a solid line with small bubbles.

Other Symbols - Refer to appendix 5 for the symbols defined by the standard.

1.7 Sensor Time Response

A sensor also has a time constant that specifies how the output changes in time when the input is changing in time. This dynamic transfer function, which is independent from the static transfer function, is often simply called the time response. It is particularly important for sensors because they are the primary element for providing knowledge of the controlled variable value.

1.7.1 First-Order Response

The simplest time response is the first order response. The time response is determined by the solution of a first-order differential equation.

Time Constant - The time constant r is part of the specification of the sensor. The time constant is sometimes referred to as the 63% time, the response time, or the e-folding time.

Real-Time Effects - The concept of an exponential time response and associated time constant is based on a sudden change of the input value. In the real world, such instantaneous changes occur rarely, if ever, and thus a worst-case situation in the time response.

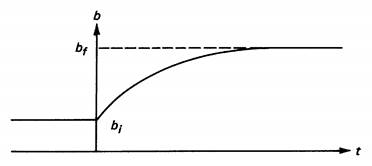
Figure 12: First-order response

1.7.2 Second-Order Response

Some sensors oscillate for a time before settling down to a value that corresponds to the new input. Such oscillation and decay is a function of the sensor. This is called a second-order response. Such a transducer will track the input when the input changes in a time that is greater than the period represented by the natural frequency. The damping constant defines the time one must wait for a disturbance at t=0 for the transducer output to be a true indication of a transducer input.

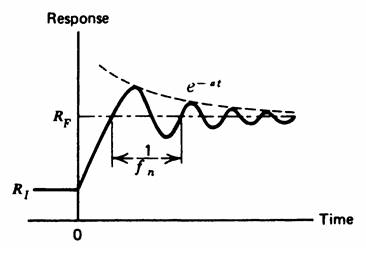
Figure 13: Second-order response

1.8 Significance and Statistics

1.8.1 Significance in Measurement

The number of significant figures is indicated either by readability, in the case of analog instruments, or by the number of digits, in a digital instrument.

Significance in Calculations - In calculations, the answer can have no more significance than the least of the numbers used in the calculation.

Significance in Design - Whenever measurement is suggested, the figures given are assumed to be the significant figures.

1.8.2 Statistics

Confidence in the value of a variable can be improved by elementary statistical analysis of measurements.

Arithmetic Mean - If many measurements of a particular variable are taken, the arithmetic mean may be calculated to obtain an average value for the variable.

Standard Deviation - Often, it is insufficient to know the value of the arithmetic mean of a set of measurements. To interpret the measurements properly, it may be necessary to know something about how individual values are spread out about the mean. The standard deviation of a group of variables will give an indication of this distribution.

Interpretation of Standard Deviation - Under certain assumptions, the standard deviation and data are related to a special curve called the normal probability or bell curve. If this is true, then 68% of all readings lie within one standard deviation of the mean, 95.5% of all readings lie within two standard deviations of the mean and 99.7% of all readings lie within three standard deviations of the mean.

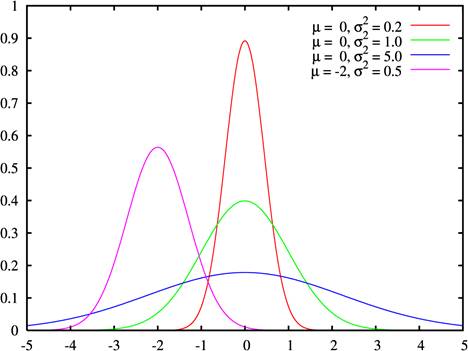
Figure 14: Four different sensors having different standard deviations.